The question of the golden section often arises among art lovers, and it causes many debates.
The golden ratio is a controversial topic in the art world. Some say it has been used by artists and architects in their creations for thousands of years. According to them, it has existed since ancient times as a means of aesthetic representation.
Proponents of the golden section say this proportion is found in the human body, as well as in the flora and fauna. Many others, on the other hand, think that it has nothing to do with aesthetics. Let me shed some light on the subject.
The answer is clearly no, the golden ratio isn't always used in art. There is no clear evidence that the golden section was intentionally used by ancient, medieval, and Renaissance painters and architects. In the 20th century, however, there are examples of the deliberate use of the golden ratio in the works of well-known artists.
The golden section is one of the best-known proportions that can be applied in art, but it is not the only one. Of course, there are other proportions and compositional systems that make a work of art or a building aesthetic.
What is the golden ratio and why is it important?
Euclid defined the golden ratio as, “A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.” Only one such point can be defined for each line, and that is the golden section.
Expressed in numbers, the golden ratio is 0.619:1 = 1+0.618. the mathematical symbol of which is the lowercase Greek letter φ (Phi).
This ratio can be applied to straight lines, flat geometric shapes (rectangle, triangle, pentagon, pentagram), and spatial solids (Icosahedron, Dodecahedron).
The golden ratio is important because it has become one of the well-known artistic composition systems over time. It was considered aesthetical by artists such as Salvador Dali or Le Corbusier. That is why I consider it important to gain some knowledge about it.
The Fibonacci sequence
Within maths, the golden ratio is most closely related to the Fibonacci number sequence.
Leonardo da Pizza, also known as Fibonacci, described this series of numbers in his book Liber Abaci when analyzing the reproduction of rabbits. It is interesting to note that it was Fibonacci who introduced Arabic numerals in Europe.
The Fibonacci sequence is an ascending series of numbers in which each number is the sum of the previous two numbers: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …
Dividing any number in the series by the number following it, the result is approximately 0.618. If we divide the number by the one before it, we get 1,618. We can observe that these are the proportions of a straight line cut in two according to the golden ratio.
The golden section can also be expressed in the following ratios: 3: 5, 5: 8, and 8:13, which correspond to consecutive numbers in the Fibonacci sequence.
Kepler recognized the relationship between the Fibonacci number sequence and the golden ratio when he realized that as the numbers increased, their ratios became closer to the value of Φ.
The Fibonacci series is often found in natural spiral patterns such as the arrangement of sunflower seeds, daisy and rose petals, pineapple, and fir cone scales.
How do you draw the golden ratio?
There are many ways to construct a golden ratio. Let’s look at two methods now:
1. Dividing a line
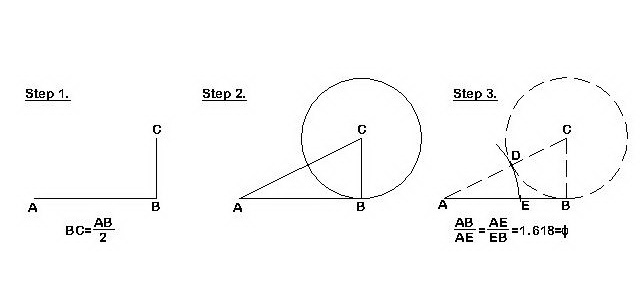
Step 1: Draw a line segment AB of any length. From point B, draw a perpendicular line with a length equal to half the length of segment AB. Mark the endpoint of the new segment with C.
BC = AB/2
Step 2: From point C obtained in this way, draw a circle with a radius r = BC. Connect points A and C with a line. Let D be the point where the circle intersects this segment.
Step 3: Draw a circle with center A and radius AD. Let E be the point at which this arc intersects segment AB. Point E divides our AB segment according to the golden ratio.
2. Constructing the golden rectangle
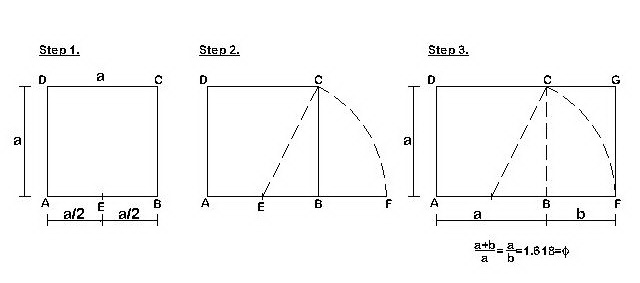
Step 1: Draw an ABCD square of any size. Halve the AB side and mark the new point with
Step 2: Draw an arc with the center point E and the radius equal to the length of the EC segment as shown below. Extend segment AB to intersect the arc.
Step 3: Extend the DC side of the square and draw a perpendicular from point F to complete the rectangle. The AFGD rectangle thus constructed corresponds to the proportions of the golden ratio.
You can also construct other geometric shapes according to the golden ratio, such as the golden spiral, triangle, pentagon, and pentagram.
Did the Egyptians know about the golden section?
Built around 2550 BC, the Great Pyramid of Giza is the only one of the Seven Wonders of the ancient world that still exists today. It was the tallest building in the world for 3,000 years before the Eiffel Tower was built.
According to Wikipedia, the pyramid of Khufu was originally 280 royal cubits (146.7 meters, 481.4 feet) high and its sides were 440 cubits (230.6 meters, 756.4 feet) long.
According to some opinions, the divine ratio was used in the construction of the Great Pyramid of Giza. However, there is no concrete evidence for this. It’s much more likely that the golden ratio wasn’t used in ancient Egyptian architecture because it was not known yet.
To determine angles and slopes, the Egyptians used seked, as evidenced by two mathematical papyri (the Rhind Mathematical Papyrus in the British Museum and the Moscow Mathematical Papyrus in the Museum of Fine Arts). Seked was also probably used in the construction of the Khufu pyramid, which determined the angle of inclination of the sides.
Was the Parthenon built according to the golden ratio?
The construction of the Parthenon began in 447 BC when Athens lived its golden age under Pericles. Under the direction of architects Ictinus and Callicrates and the sculptor Phidias, the work was completed in 432 BC.
The Greeks may have known the golden section when the Parthenon was built, but presumably, it was not used in its construction. The elements of the eastern façade of the Parthenon that many say approach the proportions of the golden section were probably not deliberately made in this way. There is, however, another proportion that is repeated several times in the construction of this magnificent temple.

According to Worldhistory.org, the floor plan of the Parthenon is 30.88 meters (101.34 feet) long and 69.5 meters (228.14 feet) wide, which means a 4: 9 aspect ratio. This ratio also occurs in other parts of the building, such as the height and width of the whole building and the width and length of the inner cell.
Did Leonardo da Vinci use the divine ratio?
Leonardo da Vinci was a good friend of Luka Pacioli. He probably encountered the golden ratio when he made the illustrations for Pacioli`s De Divina Proportione.
Although many discover the golden section in Leonardo da Vinci’s paintings, such as the face of the Mona Lisa, there is no clear evidence that Leonardo consciously applied this ratio in his drawings and paintings.
Examples of the golden ratio in art
We cannot prove with certainty that the golden section was intentionally used in the works of Renaissance artists. However, in the case of the paintings listed below, there are some proportions that are close to the divine ratio:
Birth of Venus by Sandro Botticelli. The size of the canvas is approximately the size of the golden section, as well as the placement of certain key elements of the composition.

The woodcuts for the illustration of the Apocalypse by Albrecht Dürer are also said to contain the golden ratio.

Albrecht Dürer was also of the opinion that mathematics was related to art. During his travels in Italy, he encountered works by Euclid and Pacioli which had a great influence on him. However, there is no evidence that he intentionally used the golden ratio in his compositions.
Salvador Dali consciously used the golden section as part of the composition in his famous painting The Sacrament of the Last Supper. The painting belongs to the collection of the National Gallery of Art. The dimensions of the canvas are proportional to the golden rectangle. There is also a dodecahedron in the upper part of the picture, which consists of pentagons constructed according to the divine ratio.
The famous Swiss-born French architect Le Corbusier (1887-1965) also consciously used the golden ratio when creating his anthropometric ratio system, the Modulor, which he used in the design of many buildings.

Who was the first to define the golden ratio?
The antiquity
Euclid was a Greek mathematician from Alexandria. He wrote the Elements around 300 BC. This book, which included all the knowledge of mathematics to date, has since been published in more than 1,000 editions and is still valid and in use today.
Euclid’s book contains several figures constructed by using a line divided into “an extreme and mean ratio,” which today is called the golden ratio. According to Euclid, a straight line is cut into two parts “in extreme and mean ratio” when, as the whole line is to the larger segment so is the larger segment to the smaller.
Later, during the Renaissance, the golden section came back into focus.
The Renaissance
Piero della Francesca studied painting and was skilled in mathematics, writing books on, among other things, perspective and geometric solids. He also used the golden ratio to solve mathematical problems.
Luka Pacioli was an Italian mathematician and a Franciscan monk. In 1509 he wrote a book entitled The Divine Proportion (De Divina Proportione) illustrated by Leonardo da Vinci.

In his book, Luka Pacioli used information he gained from Piero della Francesca’s books.
At the beginning of De Divina Proportione, Pacioli expresses his intention to reveal the secret of harmonious forms through the golden ratio. It was through this book that the golden section found its way from math to the arts.
Johannes Kepler, the famous German mathematician commented on the golden ratio as follows:
“Geometry has two great treasures; one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold; the second we may name a precious jewel. ”
The 19th century
The terms golden ratio and golden section began to be used in the 19th century. The term Golden section (Goldener Schnitt) was first used by the German mathematician Martin Ohm.
Final thoughts
The golden ratio has been known since antiquity and is considered by many to be the ultimate means of aesthetic representation. Other opinions suggest that there is no evidence that the golden section is related to aesthetics.
There are enthusiastic supporters and opponents of the application of the golden ratio in the fine arts. Based on the information described above, I encourage you to form your own opinion on this controversial subject.
If you wish to find out more about the golden ratio, I recommend Mario Livio’s excellent book “The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number”.

Debora
My name is Debora, and I’m the founder of Drawing Fundamentals. I work as a civil engineering technician. I acquired the basic knowledge necessary for freehand and technical drawing during my school training, further developing and perfecting these skills throughout my years in the profession. Through my blog, I aim to assist anyone interested in learning to draw.

